Biologia e Matemática: uma relação de contribuição mútua

Imagine que você possui uma cultura de bactérias que está cuidando há um dia e que gostaria de saber qual o tamanho da população neste momento. Será complicado contá-las uma a uma, não é mesmo? Mas se você souber quantas bactérias você tomou para iniciar sua cultura, então podemos aproximar uma resposta para esta pergunta com a ajuda da Matemática, por meio de um modelo matemático.

Modelo matemático é o nome que damos para uma representação matemática das relações de um determinado fenômeno. Ele pode envolver diferentes elementos matemáticos como equações, funções, tabelas, gráficos, matrizes... Há também modelos que envolvem elementos mais avançados como equações diferenciais e fractais. Elaborar um modelo exige criatividade e conhecimento tanto de matemática como do fenômeno. É preciso identificar as variáveis relevantes e, muitas vezes, assumir hipóteses com relação ao fenômeno, deixando-o mais simples. Nossa situação inicial pode nos servir como um exemplo.

Um dos primeiros modelos matemáticos elaborados para descrever o crescimento de uma população foi o modelo de Malthus. Este modelo parte do pressuposto de que o número de indivíduos em um determinado instante de tempo t é proporcional ao quanto a população aumentou (ou diminuiu) do instante anterior para o atual. Por trás deste pressuposto está uma hipótese importante: as condições para o desenvolvimento desta população são ideais, ou seja, há alimento suficiente para todos os indivíduos, não existem limitações de espaço, não ocorrem situações que possam causar danos à população, etc. Neste caso, a função exponencial P(t)=P0·e(k·t) nos informa a quantidade de bactérias no instante t, onde P0 é quantidade inicial de bactérias e k é uma constante dada pela taxa de natalidade menos a taxa de mortalidade dos indivíduos, em geral determinada empiricamente.

No caso da nossa cultura de bactérias, vamos supor que comecemos com 100 indivíduos. Então, a função que representa a quantidade de bactérias em nossa cultura será dada por P(t)=100·e(k·t). O valor de k nos diz quão rápido a população cresce. Podemos estimá-lo da seguinte maneira: suponha que após uma hora, cada uma das bactérias se reproduziu e gerou mais um indivíduo. Assim, após uma hora teremos 200 bactérias. Mas, em geral, sempre há uma porcentagem que morre, digamos 1%. Desse modo, após uma hora temos: 200-0,01×200=198 bactérias. Então, P(1)=198=100·e(k·1). Resolvendo esta equação obtemos: 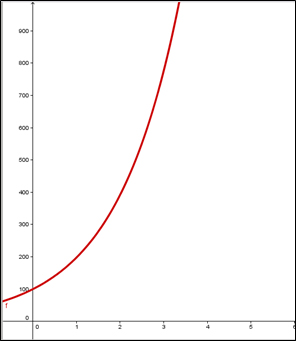Portanto, nossa função fica: P(t)=100·e(0,6831·t) e, assim, podemos determinar o número de bactérias 24 horas após o início da cultura por P(24)=100·e(0,6831·24)˜1.318.249.011 bactérias, isto é, mais de um bilhão de bactérias! Este número é surpreendente, não é? Ele pode ser explicado pelo comportamento geral da função. A imagem a seguir (Fig.1) apresenta o gráfico da função que descreve a quantidade de bactérias nas condições que estipulamos. Note que a função é sempre crescente e que em um pouco mais de 3 horas após o início da cultura, a população de bactérias já chega próximo a 900!

Este comportamento de crescimento perpétuo reflete a hipótese de condições ideais a qual nos referimos anteriormente. Com espaço abundante, alimento suficiente e sem interferências prejudiciais à população, as bactérias se reproduzem livremente, gerando o aumento exponencial da população.

Infelizmente, sabemos que esta não é a realidade do nosso fenômeno. Nossa cultura está sendo desenvolvida em uma placa de Petri, um ambiente com limitações espaciais. Além disso, apesar de estarmos alimentando nossa cultura no momento atual, pode ser que tenhamos compromissos e que nos esqueçamos de cumprir esta tarefa, afetando o desenvolvimento de algumas bactérias... 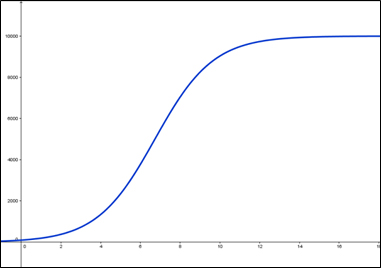Figura 1: Gráfico para a quantidade de bactérias na cultura, segundo o modelo de Malthus.

Deste modo, este modelo não está aproximando nossa situação da forma como desejamos. Um modelo que melhor aproxima as condições que enfrentamos é o modelo de Verhulst. Ele considera limitações do ambiente, como as limitações de espaço. O gráfico a seguir (Fig.2) representa o comportamento da função que descreve a população de bactérias da nossa cultura seguindo este modelo, nas mesmas condições utilizadas anteriormente. 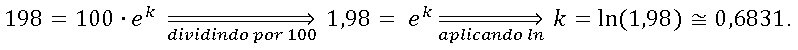Figura 2: Gráfico para a quantidade de bactérias na cultura, segundo o modelo de Verhulst.

Note que, inicialmente, o crescimento da população ainda é acentuado, uma vez que para um número inicial de bactérias a quantidade de alimento e principalmente o espaço são suficientes. Entretanto, após determinado tempo, a placa de Petri começa a se tornar pequena para a quantidade de bactérias na nossa cultura, ou seja, a quantidade de bactérias começa a alcançar uma quantidade máxima que o ambiente pode suportar. Sendo assim, a velocidade de crescimento da população diminui e a quantidade de bactérias se aproxima de um valor limite.

É importante notar as limitações dos modelos matemáticos, uma vez que sempre devemos ter em mente que um modelo apenas aproxima o fenômeno que estudamos, mas não o descreve com total fidelidade. Apesar disto, os modelos matemáticos são úteis para as diferentes áreas do conhecimento, na medida em que auxiliam na compreensão do modo como o fenômeno evolui, no modo como determinados fatores influenciam esta evolução e na elaboração de previsões sobre o fenômeno.

Particularmente, a Biologia é uma ciência que possui fenômenos bastante complexos, em geral, uma vez que frequentemente suas variáveis assumem um comportamento aleatório e são sensíveis a pequenas mudanças. Apesar disto, matemáticos e biomatemáticos possuem um grande interesse pela elaboração de modelos matemáticos para estes fenômenos, pois este trabalho auxilia no desenvolvimento e aprendizado da própria Matemática.

Neste sentido, os modelos matemáticos contribuem com a Biologia, na medida em que auxiliam no entendimento de relações existentes em seus fenômenos, na sua evolução e na tomada de decisões. Por outro lado, a Biologia contribui para o desenvolvimento da Matemática, uma vez que novos conceitos e teorias matemáticas podem ser elaborados para lidar com fenômenos biológicos que não possam ser tratados com o ferramental matemático existente. Deste modo, ambas as ciências trazem contribuições uma para a outra.

Débora da Silva Soares, Doutoranda em Educação Matemática/ GPIMEM / IGCE/ Unesp, Rio Claro