A sequência da natureza e a matemática de Fibonacci

Leonardo de Pisa nasceu por volta de 1175 na Itália e se tornou um dos mais importantes matemáticos da história. Durante sua vida, Fibonacci, como ficou conhecido por ser filho de Guglielmo dei Bonacci, contribuiu para ciência com estudos de álgebra, geometria e também aritmética. Ele recebeu os créditos por ter introduzido na Europa os algarismos indo arábicos que conhecemos hoje e a proporção áurea, presente em obras arquitetônicas famosas e supostamente na natureza.

Em seu livro Liber abaci, traduzido como "Livro do cálculo", o matemático escreveu sobre como resolver cálculos, equações e explicou o problema hipotético dos pares de coelhos, o qual se tornou um de seus problemas mais famosos e que ainda gera muitas controvérsias no mundo da ciência.

"Um casal de coelhos pode reproduzir-se após dois meses de vida e, a partir daí, produz um novo casal a cada mês. Começando com um único casal de coelhos recém-nascidos, quantos casais existirão ao final de um ano?"

A resolução do problema deu origem à sequência infinita conhecida como sequência de ouro: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55... Nela, o número seguinte na sequência é o resultado da soma dos dois números anteriores. Viu-se também que a divisão de um número e seu antecessor ao longo da sequência se aproxima cada vez mais do número de ouro (Φ), com valor aproximado de 1,61803. Esse número é obtido a partir do cálculo da razão áurea, expressa pela fórmula (a+b)/a = a/b = Φ. 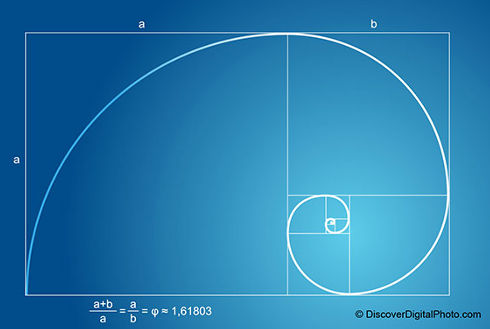Espiral áurea

Utilizando os números da sequência de Fibonacci, é possível construir um retângulo e, a partir dele, uma espiral, conhecida como espiral áurea. Tanto a espiral, quanto a proporção de ouro são conhecidas por estarem presentes em trabalhos de artistas como Leonardo da Vinci, Salvador Dalí, em conchas de alguns moluscos e na filotaxia (estudo da disposição de folhas e flores em plantas).

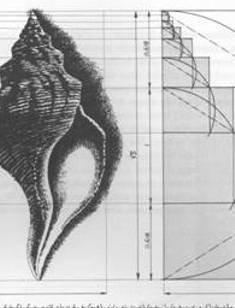
A concha do molusco nautilus é, talvez, o exemplo mais famoso nesse assunto, mas hoje sabemos que ela não é uma espiral áurea, como já mostrado por Clemente Falbo no artigo "Espirais da concha do mar" publicado na Science. A confusão ocorre porque ela se encaixa na categoria de espiral logarítmica, na qual a espiral áurea também se encontra.

No campo das artes, teoriza-se que obras nas quais a proporção é usada são mais atraentes e harmônicas visualmente.

Na botânica, plantas com 3, 5, 8 e 13 pétalas são as mais comuns. Apesar disso, existem muitas outras com números que não se encaixam na lista. Por outro lado, em capítulos de plantas da família Asteraceae, as flores estão dispostas em espirais e o número de parásticas voltadas para a direita e para a esquerda são, por vezes, números seguidos da sequência de Fibonacci. Já foi estudado também que o ângulo de crescimento de folhas pode ter o valor do ângulo áureo (157,5º) para aumentar a captação de luz.

Há aqueles que consideram a sequência de Fibonacci divina e acreditam que todo o universo é regido por ela. Há outros que afirmam que a presença desses números jamais pode ser entendida como um padrão. Embora os estudos desse cientista tenham grande importância e reconhecimento no campo das ciências exatas, não sabemos de forma segura se a razão áurea representa uma lei na natureza. Seria ela talvez uma tendência? Ou mera casualidade?

Arthur de Lima Silva - Jornal Biosferas