
Mineralogia Óptica.html
 |
Mineralogia Óptica.html |
![]()
O índice de refração:
Quando a luz passa de um meio para
outro, sua velocidade aumenta ou diminui devido as diferenças das estruturas atômicas
das duas substâncias, ou de suas densidades ópticas ou índices de refração.
O índice de refração absoluto de um meio pode ser obtido experimentalmente e é dado
pela relação:
|
onde: c= velocidade da luz na vácuo e v= velocidade da luz para um comprimento de onda específico num certo meio |
O índice de refração da luz no vácuo é considerado arbitrariamente como sendo igual a 1, que é praticamente aquele obtido para o ar: 1,00029 (temperatura de 15o C e 1 atm de pressão). De fato, tratamos o índice de refração de um mineral de forma relativa, comparando-o com o do vácuo (ou ar), ou seja, quantas vezes o seu índice de refração é maior do que aquele do vácuo, e portanto uma grandeza adimensional, que é derivado da expressão:
Da expressão (2), nota-se que o
índice de refração de um mineral é inversamente proporcional a velocidade de
propagação da luz em seu interior, ou quanto mais denso opticamente for o mineral, menor
será a velocidade de propagação da luz.
De fato, a densidade óptica, ou índice de refração do mineral é diretamente
proporcional a sua densidade, obedecendo a seguinte relação:
n -1= Kr |
onde: n= índice de refração do mineral, K= uma constante, r = densidade do mineral. |
Ainda podemos relacionar o índice de refração, a velocidade de propagação e o comprimento da onda da luz:
![]() (3)
(3)
Determinações precisas do índice de refração, empregam fontes de luz fortemente monocromáticas, no caso lâmpadas com filamento de sódio l = 589 mm . Por outro lado, emprega-se também de forma rotineira, fontes policromáticas, como é o caso do microscópio petrográfico, onde procura-se reconstituir a luz branca utilizando-se de filtros específicos para que sejam preservadas as cores naturais dos minerais. Veja na figura abaixo, como varia o índice de refração de uma placa de vidro borossilicato em função da variação dos comprimentos de onda (l) dos raios de luz que a atravessam.
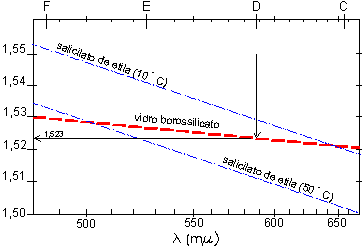
Diagrama que mostra a variação dos índices de refração em função dos
diferentes comprimentos de onda. (em mm ) F, E, D e C, correspondem às linhas de absorção de Fraunhofer
(1814).
Por convenção, em óptica cristalina,
os índices de refração dos minerais são reportados para um comprimento de onda
específico, l = 589 mm (ou 5890 Å ) que corresponde a uma das linhas de absorção de
Fraunhofer (1814) para a luz solar – nD (linha D na figura ). Além disso,
este comprimento de onda (D) corresponde a luz emitida pelo sódio que também é o valor
médio do espectro da luz visível. Com isso, e no caso do exemplo apresentado na Figura
acima, o índice de refração da placa de vidro seria 1,523.
O mesmo diagrama, mostra também a dependência do índice de refração de substâncias
cristalinas com a variação da temperatura. A Tabela abaixo, mostra os índices de
refração de algumas substâncias comuns, à 20o C:
| Substância | Índice de refração (n) |
| água | 1,333 |
| álcool etílico (anidro) | 1,362 |
| acetona | 1,357 |
| querosene | 1,448 |
| Nujol (óleo laxante) | 1,477 |
| Bálsamo do Canadá | 1,537 |
Os índices de refração dos minerais não opacos mais comuns variam entre 1,326 (vilaunita) até 2,415 (goetita). Cerca de 56% deles, situam-se entre 1,475 e 1,700 (Fleischer et al., 1984). Portanto, é plausível utilizar-se de um meio de imersão em análises ópticas como o Bálsamo do Canadá, uma vez que seu índice de refração é igual a 1,537, ou seja, próximo ao ponto médio deste intervalo.
![]()