Mineralogia Óptica.html

Princípios de interferência da luz:

Para analisarmos o fenômeno de interferência entre ondas de luz, vejamos o comportamento físico de duas ondas de luz distintas, polarizadas em um mesmo plano ou em planos diferentes.

Ondas polarizadas em um mesmo plano

A figura abaixo mostra um trem de ondas de um raio de luz que se propaga segundo a direção "OP". Os vetores representados pelas letras "a1", "a2" e "a3" apresentam a mesma direção, sentido e mesma amplitude de vibração. O mesmo ocorre para os pontos "b1", "b2" e "b3".Diz-se então que os vetores "a" (também os "b") estão em fase entre si.

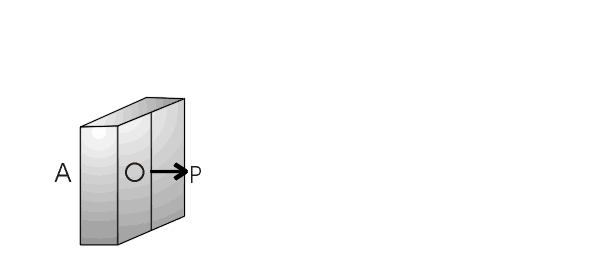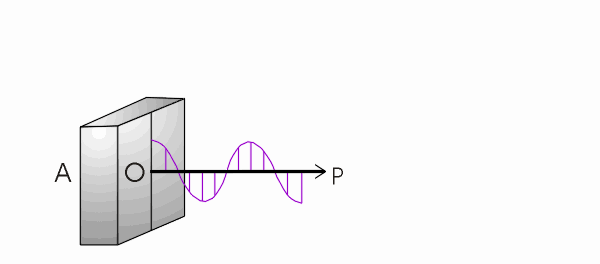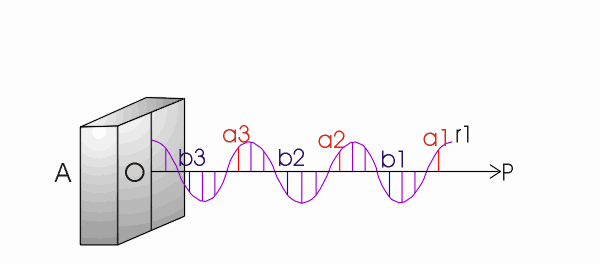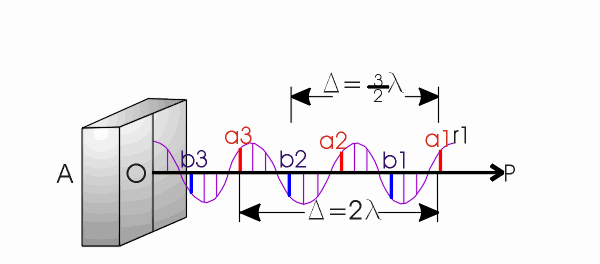
Legenda: Representação esquemática de um raio de luz "OP" polarizado verticalmente mostrando a diferença de percurso ou atraso (D) para um conjunto de pontos em fase (ex: a1, a2 e a3) e fora de fase (ex:.a1 e b1).

Por outro lado, os vetores a1 e b1, têm a mesma direção, amplitude porém sentidos opostos de vibração, ou simplesmente, estão fora de fase entre si, como mostra a figura acima. Denomina-se a distância entre dois pontos dentro de um mesmo trem de onda como diferença de trajetória ou diferença de percurso ou atraso (D) que é expressa em unidades de comprimento de onda (Å ou mm ). Então a distância entre pontos que estão todos em fase entre si será sempre um número inteiro de comprimentos de onda :

 Se admitirmos agora duas ondas de luz vibrando em um mesmo plano, sabe-se que elas não permanecem isoladas mas sim, interferem ou combinam-se para produzirem um movimento composto. Esta combinação, se faz através da soma vetorial entre as direções de vibração de cada onda independente (ou ondas primárias), ponto a ponto, produzindo uma onda resultante, conforme mostra a figura abaixo onde, por exemplo, a soma dos vetores 1’ e 1" resulta em um vetor nulo, enquanto que a soma vetorial 2’ e 2" resulta no vetor 2.

Legenda – Representação esquemática de dois raios de luz primários r1 e r2, que vibram em um mesmo plano vertical estando defasadas em 35/8l. No destaque, a resultante obtida pela soma vetorial entre os vetores individuais. Observe que a onda resultante "R" é destrutiva pois possui sua amplitude "A" é menor do que as ondas primárias.

A onda resultante da interferência entre duas ondas de luz depende do comprimento de onda, da amplitude e da diferença de percurso D entre as ondas primárias.

No caso de duas ondas primárias de mesmo comprimento de onda (l) , mas com uma diferença de percurso nl , teremos:

interferência construtiva : quando, a onda resultante apresenta uma amplitude (A) maior do que a das ondas primárias. Isto ocorrerá quando as ondas em interferência estão em fase, ou seja, "n" é um número inteiro.

interferência destrutiva: ou seja, a onda resultante apresenta uma amplitude (A) menor que do que as duas ondas primárias. Isto ocorrerá quando as ondas em interferência estão fora de fase, ou seja, "n" é um número fracionário.