Mineralogia Óptica.html

Cálculo da diferença de trajetória, percurso ou atraso (D):

A luz polarizada incidindo sobre a superfície de um mineral anisotrópico colocado na platina do microscópio, ao atravessá-lo será desdobrada em dois raios que vibram em planos perpendiculares entre si. Estes dois raios, no caso mais geral, possuem velocidades de propagação diferentes, proporcionais aos raios rápido e lento. Suponha que a velocidade de propagação do raio rápido no mineral seja igual a "V" e a do raio lento "v", cujos índices de refração seriam então, respectivamente, "n"e"N", sendo V > v e tr > tl.

Supondo tr e tl, respectivamente os tempos gastos para que os raios rápido e lento atinjam a superfície do cristal de espessura igual a "e" e como tr < tl, o mineral terá promovido um atraso, ou uma diferença de percurso D entre estes dois raios, ou seja, quando o raio lento atingir a superfície superior do mineral, o rápido já teria percorrido uma distância no ar, proporcional a D, conforme mostra a figra abaixo e D seria então:

(1) D= c (tl – tr)

onde: c= velocidade da luz no ar ou vácuo

A velocidade dos raios rápido e lento do mineral, seriam então:

(2)

Substituindo-se (2) em (1) teremos:

(3)

ou então:

(4)

mas:

(5)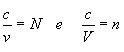

E finalmente, substituindo (5) em (4) temos:

D= e (N- n) (6)

A equação (6) indica que a diferença de trajetória ou atraso entre os raios rápido e lento ao atravessarem o mineral (D), é função de sua espessura (e) e da diferença entre os índices de refração das suas diferentes direções privilegiadas (N-n). O atraso é dado normalmente em mm .

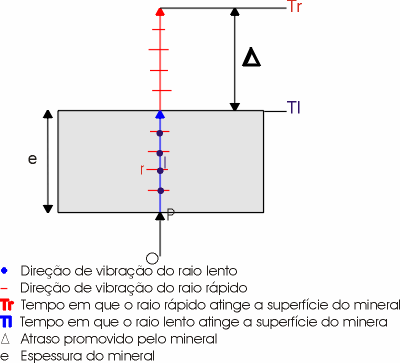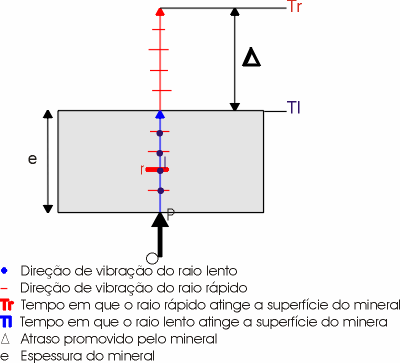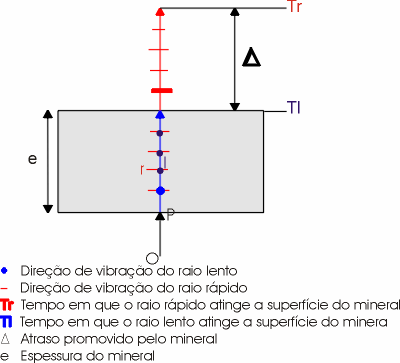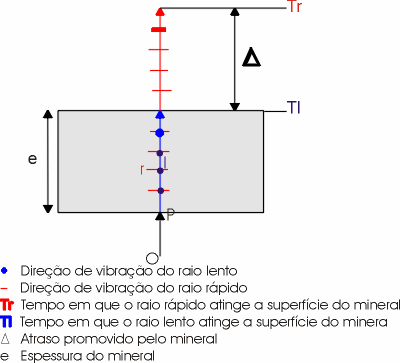
Legenda – Um raio de luz (OP), ao atingir a superfície inferior do mineral sofre dupla refração, surgindo dois raios, um lento que vibra no plano de incidência e o rápido (r) ortogonal ao primeiro. O raio rápido atinge as superfícies do mineral em um tempo Tr. Quando o raio lento atinge esta superfície, em um tempo Tl, o raio rápido terá percorrido uma distancia D, provocada pelo mineral. Observe que ambos os raios tem comportamento ordinário.