Mineralogia Óptica.html

Cores de interferência:

As cores de interferência exibidas por um fragmento de mineral, a nicóis cruzados, são devidas às diferenças de percurso ( D ) provocadas pelo mineral aos dois conjuntos de onda que emergem do cristal e vibram em planos ortogonais entre si. Desta forma, como mostra a equação D= e (N-n) o atraso, ou a cor de interferência de um certo grão mineral (D), será proporcional à sua espessura (e) e a diferença entre os seus índices de refração (birrefringência = N-n= d ).

Observe que esta expressão corresponde a equação de uma reta, onde podemos escrever:

onde no eixo das abcissas estão representados os valores do atraso (D); no das ordenadas os valores das espessuras (e) e (N-n) corresponde ao coeficiente angular da reta, conforme mostra a figra abaixo. Observe que a reta representada por esta equação passaria pela origem, pois o valor de "b" da reta seria igual a zero.

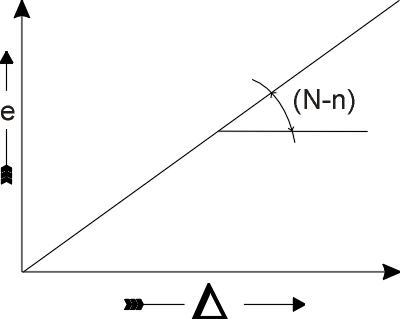
Legenda – Representação gráfica da equação D = e(N-n), que configura uma reta. É nesta equação que se baseia a carta de cores de interferência.

Variando-se dois coeficientes desta expressão, podemos obter um conjunto de retas acompanhada de um conjunto de cores de interferência conforme mostrado na figura abaixo, que constitui a chamada carta de cores de Michael - Levy.

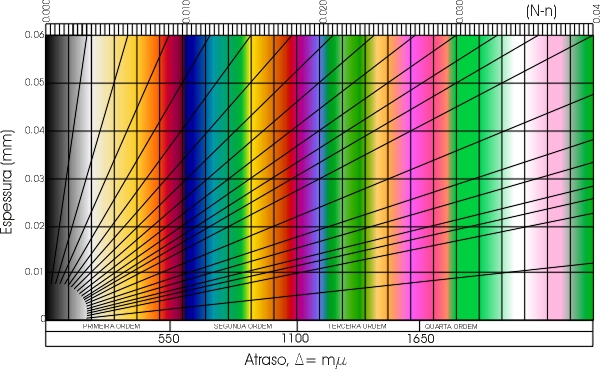
Legenda – Principais elementos que constituem a carta de cores. Observe que cada ordem corresponde a um intervalo de 550mm (corresponde a média dos comprimentos de onda da luz visível que é, aproximadamente o comprimento da onda emitida por uma fonte de luz monocromática de vapor de sódio).

Assim, as cores de interferência produzidas por diferença de percurso:

D = 0 - 550 mm - Cores de 1ª ordem – preto, cinza, amarelo, laranja e vermelho;

D = 550 - 1100 mm - Cores de 2ª ordem – violeta, azul, verde, amarelo, laranja, vermelho

D = 1100 - 1650 mm - Cores de 3ª ordem – azul, verde, amarelo, vermelho

D > 1650mm - Cores de 4º ordem e acima – tonalidades de verde e vermelho

Cada ordem que consiste a carta de cores de Michael-Levy, é separada pela cor vermelho que se repete a cada intervalo de um comprimento de onda ou 550 mm. Observe que  há também varias cores que se repetem, como exemplo do amarelo; 1^a ordem (D = 260mm), 2ª ordem (D = 890mm) e 3ªordem (D = 1140mm). Há também o caso de cores que são observadas apenas em uma ordem é o caso do preto e da cor cinza, e suas tonalidades, que ocorrem apenas em 1^a ordem.

A repetição de certas cores de interferência em diferentes ordens pode ser explicada através de um mineral anisotrópico em forma de cunha, ou seja, com espessura variável de forma contínua, conforme mostra a figura abaixo. Enquanto a espessura da cunha produzir uma diferença de fase igual a

haverá passagem de luz através do analisador a uma taxa de transmissão "T" igual a :

T = (sen² 180ºi)x100

onde i = número inteiro correspondente a diferença de fase entre os raios de luz lento e rápido que deixam o mineral.

Esta expressão é válida se admitirmos que os polarizadores estão orientados a 90º entre si e o mineral esta em sua posição de máxima iluminação. Observe que "T" assume um valor máximo quando:

com n sendo um número inteiro qualquer, ou seja quando a interferência da luz assume um caráter destrutivo.

Por outro lado, quando i = nl, ou seja, a interferência entre dois raios de luz que deixam o mineral é construtiva, conforme mostra a figura abaixo, com "T" = 0, não haverá passagem de luz pelo analisador.

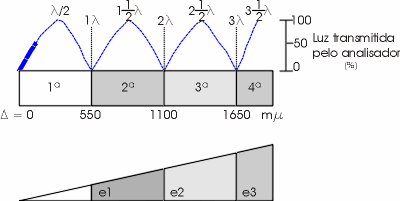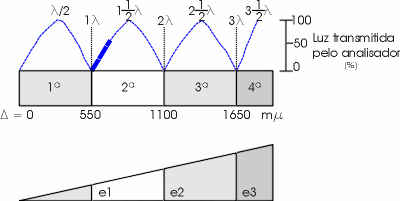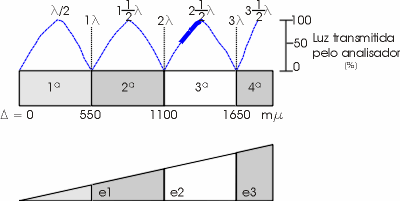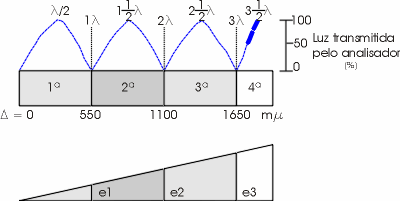
Legenda – Cunha de um mineral anisotrópico observada a nicóis cruzados mostrando que quando sua espessura (e) for tal a produzir uma interferência construtiva (nl) não haverá passagem de luz pelo analisador ao contrário quando a interferência for destrutiva ou seja .